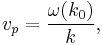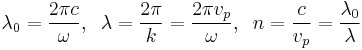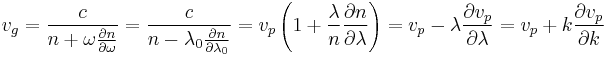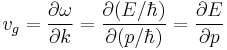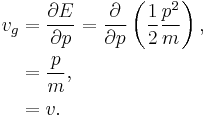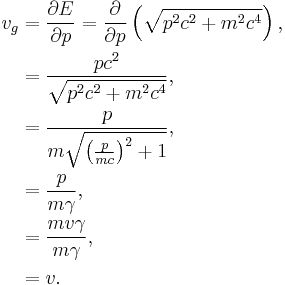Group velocity
The group velocity of a wave is the velocity with which the overall shape of the wave's amplitudes — known as the modulation or envelope of the wave — propagates through space.
For example, imagine what happens if a stone is thrown into the middle of a very still pond. When the stone hits the surface of the water, a circular pattern of waves appears. It soon turns into a circular ring of waves with a quiescent center. The ever expanding ring of waves is the wave group, within which one can discern individual wavelets of differing wavelengths traveling at different speeds. The longer waves travel faster than the group as a whole, but they die out as they approach the leading edge. The shorter waves travel slower and they die out as they emerge from the trailing boundary of the group.
Contents |
Definition and interpretation
Definition
The group velocity vg is defined by the equation
where ω is the wave's angular frequency (usually expressed in radians per second), and k is the angular wavenumber (usually expressed in radians per meter).
The function ω(k), which gives ω as a function of k, is known as the dispersion relation. If ω is directly proportional to k, then the group velocity is exactly equal to the phase velocity. Otherwise, the envelope of the wave will become distorted as it propagates. This "group velocity dispersion" is an important effect in the propagation of signals through optical fibers and in the design of high-power, short-pulse lasers.
Note: The above definition of group velocity is only useful for wavepackets, which is a pulse that is localized in both real space and frequency space. Because waves at different frequencies propagate at differing phase velocities in dispersive media, for a large frequency range (a narrow envelope in space) the observed pulse would change shape while traveling, making group velocity an unclear or useless quantity.
Derivation
Consider a smooth peaked function α(x), for example
with Fourier transform A(k) which is assumed to a narrow function (1/σ small)
Then the wave-packet defined by
which has central wave-number k0 and frequency ω(k0), can be approximated by expanding ω(k) in the exponent in a Taylor series about k0 by
This has an "envelope" (i.e. shape of waveform)
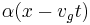 ,
,
traveling with the group velocity vg, while the phase of the wave
travels with the phase velocity
This makes clear that the "group" velocity is a useful concept only as long as the higher terms in the Taylor series expansion of ω are not important in that Fourier transform, i.e., if A(k) is sufficiently narrow a function. Those higher order terms in the Taylor series expansion of ω result in spreading of the packet and other changes to the shape of the envelope function.
Physical interpretation
The group velocity is often thought of as the velocity at which energy or information is conveyed along a wave. In most cases this is accurate, and the group velocity can be thought of as the signal velocity of the waveform. However, if the wave is travelling through an absorptive medium, this does not always hold. Since the 1980s, various experiments have verified that it is possible for the group velocity of laser light pulses sent through specially prepared materials to significantly exceed the speed of light in vacuum. However, superluminal communication is not possible in this case, since the signal velocity remains less than the speed of light. It is also possible to reduce the group velocity to zero, stopping the pulse, or have negative group velocity, making the pulse appear to propagate backwards. However, in all these cases, photons continue to propagate at the expected speed of light in the medium.[1][2][3][4]
Anomalous dispersion happens in areas of rapid spectral variation with respect to the refractive index. Therefore, negative values of the group velocity will occur in these areas. Anomalous dispersion plays a fundamental role in achieving backward propagating and superluminal light. Anomalous dispersion can also be used to produce group and phase velocities that are in different directions.[2] Materials that exhibit large anomalous dispersion allow the group velocity of the light to exceed c and/or become negative.[4][5]
History
The idea of a group velocity distinct from a wave's phase velocity was first proposed by W.R. Hamilton in 1839, and the first full treatment was by Rayleigh in his "Theory of Sound" in 1877.[6]
Other expressions
For light, the refractive index n, vacuum wavelength λ0, and wavelength in the medium λ, are related by
The group velocity, therefore, satisfies:
Matter-wave group velocity
Albert Einstein first explained the wave–particle duality of light in 1905. Louis de Broglie hypothesized that any particle should also exhibit such a duality. The velocity of a particle, he concluded then (but may be questioned today, see above), should always equal the group velocity of the corresponding wave. De Broglie deduced that if the duality equations already known for light were the same for any particle, then his hypothesis would hold. This means that
where E is the total energy of the particle, p is its momentum, ħ is the reduced Planck constant. For a free non-relativistic particle it follows that
where  is the mass of the particle and v its velocity.
is the mass of the particle and v its velocity.
Also in special relativity we find that
where m is the mass of the particle, c is the speed of light in a vacuum,  is the Lorentz factor, and v is the velocity of the particle regardless of wave behavior.
is the Lorentz factor, and v is the velocity of the particle regardless of wave behavior.
Group velocity (equal to an electron's speed) should not be confused with phase velocity (equal to the product of the electron's frequency multiplied by its wavelength).
Both in relativistic and non-relativistic quantum physics, we can identify the group velocity of a particle's wave function with the particle velocity. Quantum mechanics has very accurately demonstrated this hypothesis, and the relation has been shown explicitly for particles as large as molecules.
See also
- Wave propagation
- Dispersion (optics) for a full discussion of wave velocities
- Phase velocity
- Front velocity
- Group delay and phase delay
- Signal velocity
- Slow light
- Wave propagation speed
- Defining equation (physics)
References
Notes
- ^ Gehring, George M.; Schweinsberg, Aaron; Barsi, Christopher; Kostinski, Natalie; Boyd, Robert W. (2006), "Observation of a Backward Pulse Propagation Through a Medium with a Negative Group Velocity", Science 312 (5775): 895–897, Bibcode 2006Sci...312..895G, doi:10.1126/science.1124524, PMID 16690861
- ^ a b Dolling, Gunnar; Enkrich, Christian; Wegener, Martin; Soukoulis, Costas M.; Linden, Stefan (2006), "Simultaneous Negative Phase and Group Velocity of Light in a Metamaterial", Science 312 (5775): 892–894, Bibcode 2006Sci...312..892D, doi:10.1126/science.1126021, PMID 16690860
- ^ Schweinsberg, A.; Lepeshkin, N. N.; Bigelow, M.S.; Boyd, R. W.; Jarabo, S. (2005), "Observation of superluminal and slow light propagation in erbium-doped optical fiber", Europhysics Letters 73 (2): 218–224, Bibcode 2006EL.....73..218S, doi:10.1209/epl/i2005-10371-0
- ^ a b Bigelow, Matthew S.; Lepeshkin, Nick N.; Shin, Heedeuk; Boyd, Robert W. (2006), "Propagation of a smooth and discontinuous pulses through materials with very large or very small group velocities", Journal of Physics: Condensed Matter 18 (11): 3117–3126, Bibcode 2006JPCM...18.3117B, doi:10.1088/0953-8984/18/11/017
- ^ Withayachumnankul, W.; Fischer, B. M.; Ferguson, B.; Davis, B. R.; Abbott, D. (2010), "A Systemized View of Superluminal Wave Propagation", Proceedings of the IEEE 98 (10): 1775–1786, doi:10.1109/JPROC.2010.2052910
- ^ Brillouin, Léon (1960), Wave Propagation and Group Velocity, New York: Academic Press Inc., OCLC 537250
Further reading
- Tipler, Paul A. (2003), Modern Physics (4th ed.), New York: W. H. Freeman and Company, ISBN 0-7167-4345-0. 223 p.
- Biot, M. A. (1957), "General theorems on the equivalence of group velocity and energy transport", Physical Review 105 (4): 1129–1137, Bibcode 1957PhRv..105.1129B, doi:10.1103/PhysRev.105.1129
- Whitham, G. B. (1961), "Group velocity and energy propagation for three-dimensional waves", Communications on Pure and Applied Mathematics 14 (3): 675–691, doi:10.1002/cpa.3160140337
- Lighthill, M. J. (1965), "Group velocity", IMA Journal of Applied Mathematics 1 (1): 1–28, doi:10.1093/imamat/1.1.1
- Bretherton, F. P.; Garrett, C. J. R. (1968), "Wavetrains in inhomogeneous moving media", Proceedings of the Royal Society of London, Series A, Mathematical and Physical Sciences 302 (1471): 529–554, Bibcode 1968RSPSA.302..529B, doi:10.1098/rspa.1968.0034
- Hayes, W. D. (1973), "Group velocity and nonlinear dispersive wave propagation", Proceedings of the Royal Society of London, Series A, Mathematical and Physical Sciences 332 (1589): 199–221, Bibcode 1973RSPSA.332..199H, doi:10.1098/rspa.1973.0021
- Whitham, G. B. (1974), Linear and nonlinear waves, Wiley, ISBN 0471940909
External links
- Greg Egan has an excellent Java applet on his web site that illustrates the apparent difference in group velocity from phase velocity.
- Group and Phase Velocity - Java applet with configurable group velocity and frequency.
- Maarten Ambaum has a webpage with movie demonstrating the importance of group velocity to downstream development of weather systems.
| Velocities of waves |
|---|
| Phase velocity • Group velocity • Front velocity • Signal velocity |
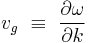
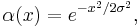
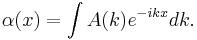
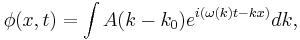
![\phi(t,x)\approx e^{i(\omega(k_0) t -k_0 x)} \int A(\delta k) exp\left[i\left(\frac{\partial\omega}{\partial k} t-x\right)\delta k\right] d\delta k =e^{i\left(\omega(k_0) t-k_0 x\right)} \alpha\left(x-\frac{\partial\omega}{\partial k} t\right)](/2012-wikipedia_en_all_nopic_01_2012/I/c4a1b0e9bb3cfd2363b46f83c6bb05bf.png)
![e^\left [ \omega(k_0)t-k_0 x \right ],](/2012-wikipedia_en_all_nopic_01_2012/I/25b2bce13aa00a6e3e9e80e5502151ed.png)